II. KAŽDÝ ŠKOLÁK VÍ
... (citace z Johna Drydena)

Věda je stejně jako umění, náboženství, obchod, válčení a  dokonce spánek, založena na předpokladech. Od jiných odvětví lidské činnosti se ale liší tím, že cesty vědeckého myšlení jsou určeny předpoklady vědců, a jejich cílem je ověřit či opravit staré předpoklady a vytvořit nové.
Přitom je samozřejmě žádoucí (i když ne absolutně nutné), aby vědec přesně znal a dokázal formulovat své vlastní předpoklady. Pro vědecký úsudek je také výhodné a nutné znát předpoklady kolegů pracujících ve stejné oblasti. Kromě toho všeho musí čtenář vědecké práce znát předpoklady jejího autora.

Přednášel jsem nejrůznější odvětví behaviorální biologie a kulturní antropologie americkým studentům od středních škol až po budoucí psychiatry, v různých školách a fakultních nemocnicích a objevil jsem v jejich myšlení velice podivnou mezeru, způsobenou nedostatkem jistých nástrojů myšlení. Tento nedostatek se vyskytuje v prakticky stejné míře na všech úrovních škol, u studentů obou pohlaví, humanitně i vědecky zaměřených. Konkrétně spočívá v neznalosti předpokladů nejen z oblasti vědy, ale i každodenního života.

Tato mezera je kupodivu méně znatelná u dvou skupin studentů, které jsou zdánlivě naprosto protichůdné : u katolíků a marxistů. Obě skupiny přemýšlejí nebo se dověděly něco málo o posledních 2500 letech lidského myšlení a určitým způsobem si uvědomují důležitost filozofických, vědeckých a epistemologických předpokladů. Obě skupiny je velmi obtížné něco učit, protože kladou tak velký důraz na "správné" premisy a předpoklady, že v herezi vidí nebezpečí exkomunikace. Samozřejmě že každý, kdo vidí v herezi nebezpečí, bude velmi bedlivě dbát na to, aby si uvědomoval své vlastní předpoklady a stane se v této oblasti do jisté míry "znalcem". Ti, kdo nikdy neslyšeli o myšlence, že je možné se mýlit, se nemohou naučit nic jiného než know-how. Námět této knihy má velice blízko k jádru náboženství a vědecké ortodoxie. Předpoklady - a většina studentů potřebuje poučit, co to takový předpoklad je - musejí být jasně vyloženy.

Je tu ale jiný problém, který se týká téměř výlučně amerického prostředí. Američané si bezpochyby hájí své předpoklady stejně nekompromisně jako kterýkoli jiný národ (a stejně jako autor této knihy), ale velice podivně reagují na jasné vyjádření jakéhokoliv předpokladu. Obyčejně je označí za nepřátelské nebo výsměšné anebo - a to je nejhorší - za autoritářské.
Proto je také možné, že v této zemi, založené na svobodě vyznání, je náboženská výchova naprosto vyřazena ze státní výuky. Členům slabě věřících rodin se nedostává jiného poučení než v kruhu rodinném. A tak formálně a jasně vyjádřit jakoukoli premisu nebo předpoklad znamená čelit slabému odporu; nikoli námitkám - neboť posluchači neznají protichůdné premisy ani nevědí, jak je vyjádřit - ale velmi kultivované hluchotě, jakou používají děti, když nechtějí slyšet, co říkají rodiče, učitelé a církevní hodnostáři. Ať tak či onak, osobně věřím v důležitost vědeckých předpokladů; věřím také v to, že existují lepší i horší způsoby, jak budovat vědecké teorie, a v to, že je nutné předpoklady jasně formulovat, aby mohly být prozkoumány a zdokonaleny.

Proto je tato kapitola věnována seznamu předpokladů, někdy známých, někdy nových pro čtenáře, kteří byli doposud uchráněni od myšlenky, že některé předpoklady jsou prostě chybné. Některé nástroje myšlení jsou tak tupé, že je prakticky nelze použít; jiné jsou tak ostré, že je nebezpečné s nimi zacházet. Ale moudrý člověk dovede zacházet s oběma. Stojí za to pokusit se předběžně stanovit určité základní předpoklady, které musejí sdílet všechny mysli, nebo naopak definovat mysl stanovením seznamu takových základních komunikačních rysů.


1. Věda nikdy nic nedokazuje

Věda někdy vylepšuje hypotézy a někdy je vyvrací. Ale důkaz, to je něco jiného a zřejmě existuje jen v říši čistě abstraktní tautologie. Občas lze říci, že jestliže jsou dány takové a takové abstraktní domněnky či postuláty, pak nutně musí následovat to a to. Ale určit pravdu o tom, co lze pozorovat nebo k čemu lze dojít indukcí na základě pozorování, to je zase něco jiného.

Řekněme, že pravda by zamenala naprosto přesnou shodu mezi naším popisem a tím, co popisujeme, nebo mezi celkovým systémem našich abstrakcí a dedukcí a nějakým celkovým pochopením vnějšího světa. Pravdy v tomto smyslu nelze dosáhnout. i kdybychom odhlédli od mezí kódování a od faktu, že náš popis bude vyjádřen slovy, čísly nebo obrazy, zatímco to, co popisujeme, je z masa a krve a pohybu, nikdy si nebudeme moci činit nárok na definitivní poznání. Běžně se to předvádí asi tímto způsobem : mějme nějakou řadu - třeba čísel nebo něčeho jiného - a předpoklad, že tato řada je nějak uspořádaná. Aby to bylo jednoduché, stanovme si řadu čísel : 2, 4, 6, 8, 10, 12 .

Teď se vás zeptám : "Jaké bude další číslo v řadě ?" Pravděpodobně odpovíte, že "14". Ale já vám řeknu : "Ne. Další číslo v řadě je 27." Jinými slovy, další krok ukázal, že generalizace, ke které jste došli na základě první série údajů - že se jedná o řadu sudých čísel - je špatná nebo je přibližná.
Pokračujme dále. Nyní vytvořím takovouto řadu : 2, 4, 6, 8, 10, 12, 27, 2, 4, 6, 8, 10, 12, 27, 2, 4, 6, 8, 10, 12, 27... Když se vás teď zeptám na následující číslo, odpovíte asi "2". Třikrát za sebou byla zopakována řada čísel od 2 do 27, a jestliže jste dobrý vědec, budete ovlivněn předpokladem nazvaným Occamova břitva neboli zákon o ekonomii myšlení, to jest preferování toho nejjednoduššího závěru vyhovujícího faktům. Tímto způsobem budete předpovídat to, co následuje. Ale jaká jsou tato fakta ? Nevíte, jak pokračují za hranicí (pravděpodobně nedokončeného) úseku, který vám byl předložen.

Domníváte se, že jste schopni předpovídat, a já jsem vás také v tomto předpokladu podpořil. Ale jedinou jistotou je pro vás (naučené) preferování nejjednodušší odpovědi a důvěra, že daná řada je skutečně nedokončená a uspořádaná. Bohužel (nebo naštěstí), nikdy nelze určit, co bude následovat. Vše, co máte, je důvěra v jednoduchost, a každý další fakt může všechno jen zkomplikovat. Nebo, řečeno jinak, pro každou řadu čísel, kterou určím, existuje vždy pár jednoduchých způsobů popisu, ale nekonečně mnoho jiných způsobů, které nejsou omezeny kritériem jednoduchosti.

Předpokládejme, že čísla jsou vyjádřena písmeny : x, w, p, n a tak dále. Tato písmena mohou zastupovat jakákoli čísla, i zlomky. Pak jen tuto řadu třikrát nebo čtyřikrát zopakuji v nějaké verbální, vizuální nebo jiné formě, třeba ve formě bolesti nebo kinestézie, a vy začnete v tom, co vám nabízím, vidět nějaký řád, uspořádání - tedy vzor (pattern) . ve vaší mysli - tak jako v mé - se tento vzor stane tématem - motivem s estetickou hodnotou. v tom smyslu bude zřejmý a pochopitelný. Ale vzor se může změnit nebo rozbít přidáním, opakováním, čímkoli, co vás přinutí k novému nazírání. a tyto změny nemohou být nikdy s absolutní jistotou předpovězeny, protože k nim nikdy předtím nedošlo.

Nevíme moc o tom, jakým směrem se bude ubírat budoucnost. Nikdy nebudeme moci říct : "Díky svému pozorování a popisu této řady jsem schopen určit její další složky." nebo "Až se příště setkám s těmito jevy, budu schopen předpovědět jejich průběh od začátku do konce." Předpověď nemůže nikdy platit stoprocentně, a proto věda nemůže dokázat žádnou generalizaci, dokonce ani ověřit jediné popisné sdělení a dojít tak ke konečné pravdě. O této nemožnosti se dá diskutovat ještě z jiných hledisek. Argument této knihy - který vás samozřejmě může přesvědčit jen pokud to, co říkám, odpovídá tomu, co víte, a který se za pár let může zhroutit nebo úplně změnit - předpokládá, že věda je způsob vnímání a dávání "smyslu" našim vjemům. Ale vnímání pracuje jen na základě rozdílů. Každá přijatá informace je nutně informace o rozdílu a každé vnímání rozdílu má své hranice. Příliš jemné nebo pomalu probíhající rozdíly nelze rozeznat. Naše vnímání je nezachytí.

To znamená, že vše, co my jako vědci můžeme vnímat, má nějaké prahové hodnoty. Co je podprahové, není nic pro nás. Vědění bude tedy v jakémkoli daném momentu funkcí prahových hodnot prostředků vnímání, které máme k dispozici. Vynález mikroskopu, teleskopu, měření času až na zlomky nanosekundy nebo vážení hmoty s přesností na milióntiny gramu - všechny tyto zdokonalené prostředky vnímání nám odhalí to, co bylo naprosto nepředvídatelné z těch hladin vnímání, kterých jsme byli schopni dosáhnout, než byly objeveny.

Nejen, že nemůžeme předvídat příští okamžik v budoucnosti;nemůžeme předvídat ani příští rozměr v tom, co je mikroskopicky malé, astronomicky vzdálené nebo geologicky starší. Jako metoda vnímání má věda - a každá věda je metodou vnímání - spolu s ostatními metodami omezené schopnosti shromaž¦ovat vnější, viditelné znaky čehokoli, co může být pravdou. Věda zkoumá, leč nedokazuje.


2. Mapa není území a jméno není jmenovaná věc

Tento princip, který získal svůj věhlas díky Alfredu Korzybskimu, je zajímavý v mnoha ohledech. Upozorňuje nás, z obecného hlediska, že když myslíme na kokosy nebo prasata, žádné kokosy a prasata v našem mozku nejsou. Ale z abstraktnějšího hlediska dokazuje Korzybskiho tvrzení, že v každém myšlení nebo vnímání nebo komunikaci o vnímání dochází k transformaci, ke kódování mezi zprávou a věcí, o které zprávu podáváme, Ding an sich . Kromě toho vztah mezi zprávou a onou tajemnou věcí, o které informujeme, mívá charakter klasifikace; věc bývá zařazována do určité třídy. Pojmenovávání je vždy třídění, a mapování je v podstatě totéž co pojmenovávání.

Korzybski mluvil vlastně z pozice filozofa a snažil se lidi přimět k tomu, aby vnesli do svého způsobu myšlení trochu disciplíny. Ale nemohl uspět. Pokud aplikujeme jeho výrok na přírodopis procesu lidského myšlení, není to už tak jednoduché. Schopnost rozlišovat mezi jménem a pojmenovanou věcí nebo mezi mapou a územím má možná jen dominantní mozková hemisféra. Ta druhá, symbolická a afektivní polovina mozku, která bývá většinou na pravé straně, není pravděpodobně schopna dělat rozdíl mezi jménem a pojmenovanou věcí. Rozhodně se takovým rozlišováním nezabývá. Proto jsou v lidském životě nutně přítomny určité neracionální typy chování. Hemisféry máme dvě, s tím se nedá nic dělat a každá pracuje poněkud jinak; z toho vyplývají různé problémy a s tím se taky nedá nic dělat.

Například, pomocí dominantní hemisféry můžeme v takové věci jako je vlajka vidět určitý druh pojmenování země nebo organizace, kterou představuje. Ale pravá hemisféra žádný podobný rozdíl nedělá a vlajka je pro ní identická s tím, co představuje. Takže vlajka USA je USA. Pokud jí někdo pošlape, odpovědí může být vztek. a ten se nijak nezmírní ani po objasnění vztahů jméno-věc nebo mapa-území. (Ostatně, člověk, který na vlajku šlape, ji také ztotožňuje s tím, co zastupuje.) Vždy a nutně bude existovat velké množství situací, v nichž reakce nebude podmíněna logickým rozlišením jména a pojmenované věci.


3. Objektivní poznání neexistuje

Každé poznání je subjektivní. To je jen nutný důsledek toho, co je naznačeno ve 4. oddílu - že obrazy, o kterých si myslíme, že je "vnímáme", vytváří náš mozek. Důležité je, že veškeré vnímání - totiž vědomé vnímání - má formu obrazu. Bolest je někde umístěna. Má začátek a konec a místo a stojí proti nějakému pozadí. To jsou základní rysy obrazu. Když mi někdo šlápne na nohu, to, co zakouším, není to, že mi šlápl na nohu, ale můj obraz jeho šlápnutí, vytvořený z informací, které neurony přenesly do mého mozku nějakou chvíli po té, co bota dotyčného přistála na mé. Poznání vnějšího je vždy zprostředkováno příslušnými smyslovými orgány a drahami neuronů. v tom případě jsou předměty mým výtvorem a moje poznání není objektivní, nýbrž subjektivní. Není ovšem zanedbatelné, že jen nepatrná hrstka lidí, alespoň v západní kultuře, pochybuje o objektivitě takových informací jako je bolest nebo zrakové vnímání okolního světa. Naše civilizace je v této iluzi pevně zakotvena.


4. Tvorba obrazu je nevědomá

Toto zobecnění platí zřejmě o všem, co se děje mezi okamžikem, kdy někdy vědomě nasměruji smyslový orgán k nějakému zdroji informací a chvílí, kdy vědomě získám informaci z obrazu, o kterém si myslím, že "já" vidím, cítím, slyším atd. Jistě i bolest je takto vytvořeným obrazem. Není pochyb o tom, že všichni, lidé, psi, osli si uvědomují, že něco poslouchají a uvědomují si i to, že nastraží uši tím směrem, odkud zvuk vychází. Co se týče zraku, stavá se, že něco, co se pohybuje na periferii mého zorného pole, vzbudí mou "pozornost" (ať už je to cokoli), takže tím směrem obrátím oči a někdy i hlavu. To bývá často proces vědomý, ale probíhá někdy tak automaticky, že ho téměř nezaregistruji. Často si uvědomuji, že otáčím hlavu, ale nevím o tom, že otočení bylo způsobeno mým periferním viděním. Periferní vidění přijímá mnoho informací, které unikají vědomí - pravděpodobně, ale ne jistě bývají v podobě obrazu.

Procesy vnímání nejsou zachytitelné; vědomé jsou pouze jejich výsledky, a jen ty jsou také pro nás nezbytné. Tyto dvě obecné skutečnosti - za prvé, že si neuvědomuji procesy vytváření obrazů, které vědomě vidím, a za druhé, že v těchto nevědomých procesech využívám celé řady předpokladů, které jsou posléze zabudovány do výsledného obrazu - to je pro mne začátek empirické epistemologie.

Samozřejmě všichni víme, že obrazy, které "vidíme", se ve skutečnosti tvoří v našem mozku nebo v naší mysli. Ale vědět to z intelektuálního hlediska je zcela něco jiného než uvědomovat si, že tomu vskutku tak je. o téhle důležité věci jsem začal chtě nechtě přemýšlet před nějakými třiceti lety v New Yorku, kde Adalbert Ames předváděl pokusy s tím, jak svým vizuálním obrazům přisuzujeme hloubku. Ames byl oční lékař a ošetřoval pacienty, kteří trpěli anisokonií, to znamená v každém oku vytvářeli jinak velký obraz daného předmětu. To ho přivedlo ke zkoumání a hledání subjektivních prvků ve vnímání hloubky. a protože je to téma důležité a je základem empirické či experimentální epistemologie, popíšu Amesovy pokusy trochu důkladněji.

Všechny experimenty měl Ames instalovány ve velkém prázdném bytě uprostřed New Yorku. Bylo jich tam asi padesát. Když jsem se na ně přišel podívat, byl jsem sám. Ames mě přivítal a pobídl mě, abych začal s pokusy pěkně od začátku, a odešel dokončit nějakou práci do místnosti, která byla zařízena jako kancelář. v bytě nebyl jinak žádný nábytek, až na dvě rozkládací židle.
Prošel jsem tedy pokusy jeden po druhém. Každý z nich byl založen na nějaké optické iluzi, ovlivňující vnímání hloubky. Základní myšlenkou celé série bylo, že používáme pět základních klíčů k vytvoření zdání hloubky v obrazech, které vytváříme, když se díváme očima na okolní svět.
Prvním klíčem je velikost (měl bych napsat přesněji : kontrast ve velikosti), to jest velikost fyzického obrazu, vytvořeného na sítnici. Samozřejmě tento obraz nemůžeme vidět, takže by bylo přesnější říci, že prvním klíčem ke vzdálenosti je úhel, který předmět svírá s okem. Ale ani tento úhel není viditelný. Klíčem ke vzdálenosti, kterou zachytí zrakový nerv, je možná změna úhlu, který předmět svírá s okem. To dokazoval pokus s dvěma balónky ve tmavém prostoru. Balónky byly stejně silně osvětleny, ale vzduch mohl volně přecházet z jednoho do druhého. Samy se nehýbaly, ale jak se jeden balónek zvětšoval a druhý zmenšoval, zdálo se, že se ten větší přibližuje a menší vzdaluje. Jak vzduch naplňoval střídavě jeden a druhý balónek, zdálo se, že se střídavě pohybují dopředu a dozadu.

Druhým klíčem je jasnost předmětu. k tomu byly použity také dva balónky, které byly stejně velké, nehýbaly se, ale byly různě osvětlovány. Toto střídavé osvětlení působilo opět zdání pohybu tak, že více osvětlený balónek se přibližoval a tmavší vzdaloval.
Potom byly tyto dva pokusy zkombinovány. Menší balónek byl více osvětlen. Tato kombinace dokazovala, že některé klíče převládají nad ostatními. Těch pět klíčů, které jsem si ten den postupně vyzkoušel, bylo : velikost, jasnost, překryv, binokulární paralaxa a paralaxa způsobená pohybem hlavy. ze všech převládal nejvíce právě poslední klíč.

Když jsem absolvoval asi dvacet nebo třicet takových testů, chtěl jsem si udělat přestávku a šel jsem se posadit do rozkládací židle. Ta se pode mnou propadla. Ames zaslechl hluk a přišel se podívat, jestli je všechno v pořádku. Zůstal pak se mnou a ukázal mi další dva pokusy.
       První se zabýval paralaxou (viz Glosář). Na stole asi pět stop dlouhém byly dva předměty, připevněné na tenkých bodcích kousek nad deskou : krabička cigaret značky Lucky Strike a na vzdálenějším konci krabička papírových zápalek. Ames mě postavil k bližšímu konci stolu a vybídl mě, abych popsal, co vidím - to znamená umístění předmětů a jejich velikost. (V každém z Amesových pokusů musíte konstatovat skutečnost, dříve než jste podrobeni iluzím.) Pak mi ukázal dřevěné prkénko s kulatým otvorem, které bylo umístěno v pravém rohu stolu na mém konci, takže jsem skrz něj viděl celý stůl. Ames mi řekl, abych se podíval a hlásil, co vidím. Samozřejmě, že oba předměty zatím byly tam, kde jsem je viděl předtím a byly stejně velké. Když jsem se díval skrz otvor v prkénku, byl jsem nucen použít jen jedno oko a neviděl jsem tedy stůl tak plasticky. Ames mi řekl, že budu-li posouvat destičkou podél hrany stolu, vznikne paralaxa.

A skutečně, jak jsem prkénko posouval, obraz se jako zázrakem změnil. Cigarety byly najednou na vzdáleném konci stolu a zdály se být dvakrát tak velké i široké, než normální balíček cigaret. i papír, z kterého byla krabička vyrobena, měl jinou strukturu. Všechny malé nerovnosti byly teď viditelnější. Krabička zápalek měla naopak trpasličí rozměry a byla asi uprostřed stolu, na místě, kde předtím stály cigarety. k čemu při posouvání došlo ? Odpověď je jednoduchá. Pod stolem byly umístěny dvě páky nebo tyče, které jsem neviděl a které posouvaly předměty současně s tím, jak jsem posouval dřevěnou destičku. Při normální paralaxi se děje, jak víme, toto : když se díváme ven z jedoucího vlaku, zdá se nám, že blízké předměty (nebo zvířata, např. krávy) se rychle pohybují dozadu. Vzdálené hory naopak ubíhají tak pomalu, že to vypadá, jako by cestovaly spolu s vlakem.

V tomto případě skryté kladky způsobily, že se bližší předmět pohyboval dopředu spolu s pozorovatelem. Krabička cigaret se potom zdála být daleko a zápalky naopak blíž. Jinými slovy, pohybem oka, spojeným s pohybem dřevěné destičky jsem vytvořil převrácený dojem a za těchto podmínek nevědomý proces tvorby obrazu stvořil ten správný obraz. Informaci o cigaretové krabičce můj mozek přečetl jako obraz vzdáleného předmětu, ale jeho výška svírala s mým okem stále stejný úhel. Proto se nyní zdála krabička být tak nepoměrně veliká. Podobně se zápalky zdánlivě přiblížily, ale svíraly s okem stejný úhel jako ze svého skutečného stanoviště. Takže jsem vytvořil obraz, v němž byla krabička zápalek o polovinu blíž a o polovinu menší, než předtím. Celá mašinérie vnímání vytvořila obraz v souladu s pravidly paralaxy, kterou poprvé jasně popsali již renesanční malíři; a celý proces vytváření obrazu za pomoci zakořeněných poznatků ze základů paralaxe probíhal naprosto mimo mé vědomí. Zákony vesmíru, o kterých si myslíme, že je dobře známe, jsou skryty hluboko v procesech našeho vnímání.

Epistemologie na úrovni přírodovědy je obvykle rovněž nevědomá, a proto je tak obtížné ji změnit. Obtížností změny se zabýval druhý pokus, při kterém mi Ames asistoval. Pokus byl nazván různoběžníkový prostor. Ames mi ukázal velikou krabici asi pět stop širokou, tři stopy vysokou a tři stopy dlouhou od přední stěny k zadní. Krabice měla zvláštní, různoběžníkový tvar a Ames mě pobídl, abych si ji dobře prohlédl a zapamatoval si její skutečné rozměry. V přední stěně krabice byl otvor, dostatečně velký pro obě oči, ale Ames mi před začátkem experimentu nasadil spektrální brýle, které měly zkreslit mé binokulární vidění. Měl jsem vytvořit subjektivní předpoklad, že mám paralaxu obou očí, zatímco ve skutečnosti jsem neměl téměř žádné binokulární vidění. Když jsem se podíval dovnitř, zdálo se, že vnitřek má zcela přesně obdélníkový tvar a vypadal jako pokoj s obdélníkovými okny. Samozřejmě, že to s nimi nebylo tak jednoduché. Okna byla nakreslena v protikladu k liniím různoběžníku tak, že měla zdánlivě obdélníkový tvar. Vnitřní protilehlá strana krabice, na kterou jsem se díval otvorem, byla šikmá (to jsem věděl z předchozí prohlídky), takže její levá část byla dál ode mě a pravá blíž. Ames mi podal hůlku a řekl mi, abych se jejím koncem dotkl papíru, který byl připíchnutý na levé stěně. To se mi lehce podařilo. Teď se Ames zeptal : "Vidíte podobný papír i na pravé stěně ? Chci, abyste se toho papíru dotkl hůlkou. Nejprve přiložte konec hůlky k papíru na levé stěně a pak udeřte, jak nejvíc můžete."

Udeřil jsem. Konec hůlky se o kousek posunul, pak narazil na zadní stěnu a dál to nešlo. Ames řekl : "Zkuste to znovu." Zkoušel jsem to snad padesátkrát, až mě začala bolet ruka. Věděl jsem samozřejmě, jak mám usměrnit svůj pohyb : při úderu bylo třeba hůlku přitáhnout víc k sobě, abych nenarazil na zadní stěnu. Ale to, co jsem skutečně dělal, bylo řízeno vytvořeným obrazem. Snažil jsem se jít proti vlastnímu spontánnímu pohybu. (Myslím, že kdybych zavřel oči, šlo by mi to líp, ale nevyzkoušel jsem to.) Papíru na pravé straně jsem se nikdy nedotkl, ale moje výkony se kupodivu postupně zlepšovaly. Nakonec jsem byl schopen hůlku o značný kus posunout, než narazila na zadní stěnu. a pod dojmem výkonů, které jsem opakoval a zlepšoval, měnil se můj obraz pokoje a nabýval stále více různoběžníkových tvarů. Ames potom potvrdil, že při delším nácviku se lidem podařilo docela snadno zasáhnout papír na pravé straně a zároveň vidět skutečný tvar pokoje.

Různoběžníkový pokoj byl v pořadí pokusů poslední. Ames mi navrhl, abychom si zašli na oběd. Šel jsem se do koupelny umýt. Otočil jsem modrým kohoutkem a vyvalil se na mne proud vařící vody smíšený s párou. Pak jsme šli ven hledat nějakou restauraci. Má důvěra ve vlastní tvorbu obrazů byla tak otřesena, že jsem skoro nebyl schopný přejít ulici. Nebyl jsem si jistý, jestli jsou auta skutečně tam, kde je vidím. Zkrátka, proti okamžitým příkazům obrazu, který vnímání vytváří v mysli, žádná svobodná vůle nic nezmůže. Ale trpělivým nácvikem a korekcí je možné tyto obrazy pozměnit. (Viz změny v kalibraci, o kterých se hovoří v 7. kapitole.)

I přes Amesovu krásnou sérii pokusů zůstává proces tvorby obrazu i nadále absolutní záhadou. Nevíme, jak probíhá, ani za jakým účelem. Je sice hezké prohlásit, že to má adaptační smysl pouze předkládat našemu vědomí již hotové obrazy a neplýtvat psychologickými procesy na uvědomování si jejich tvorby. Nevím však o žádném jasném důvodu, proč vůbec obrazy používat nebo proč si nějakou část našich mentálních procesů vůbec uvědomovat. Spekulací můžeme dojít k názoru, že tvorba obrazů je zřejmě vhodnou a úspornou metodou k převádění informací skrze mezičlánky. Zvláště v situaci, kdy člověk musí jednat v kontextu mezi nějakými dvěma přístroji, je výhodné, když se mu informace z nich dostává ve formě obrazu.

Případ tohoto druhu, který byl podroben systematickému průzkumu, je případ střelce řídícího protileteckou palbu na válečné lodi. Informace o letícím cíli z řady zaměřovacích přístrojů dostává střelec v podobě pohyblivého bodu na obrazovce (tj. v podobě obrazu). Na ní je ještě druhý bod, vyjadřující směr, kterým je namířena protiletadlová zbraň. Tento bod může střelec posouvat pomocí knoflíků na palubní desce. Knoflíky mění také střelcův cíl. Střelec jimi musí otáčet tak dlouho, až se oba body spojí v jeden. Pak vystřelí.

Systém má dva mezičlánky ('rozhraní') : senzorický systém - člověk a člověk - člověka jakožto vnímací soustavu (senzorický systém) a člověka jako soustavu výkonnou (efektorový systém). Samozřejmě by v tomto případě bylo možné vstupní i výstupní informace zpracovat digitálně, bez ikonického přenosu. Ale ikonické zprostředkování je podle mě mnohem vhodnější nejen proto, že jako lidské bytosti vytváříme mentální obrazy, ale také proto, že v těchto mezičláncích je použití obrazů ekonomické a účinné. Je-li tato úvaha správná, pak by se z toho dalo rozumně vyvodit, že savci vytvářejí obrazy, protože jejich mentální procesy procházejí přes velké množství mezičlánků.


5. Rozdělit vnímaný svět na části a celky je vhodné a možná i nezbytné,
    ale žádná nutnost nám neříká, jak to udělat

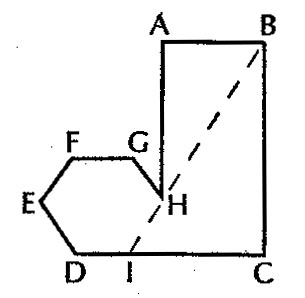
Mnohokrát jsem se snažil přiblížit tuto obecnou skutečnost svým studentům a používal jsem k větší názornosti Obrázku č. 1. Obrázek jsem třídě vždy nakreslil relativně přesně křídou na tabuli, ale bez písmen, která označují jednotlivé úhly. Potom "to" měla třída písemně popsat v rozsahu jedné strany. Když byli všichni hotovi, porovnali jsme výsledky. Bylo je možné rozdělit do několika kategorií :

a) Asi deset či méně procent studentů napsalo, že obrázek představuje např. botu, ti s větší fantazií popsali dokonce botu člověka, který má opuchlý palec, někoho napadla i záchodová mísa. Je jasné, že na základě podobného analogického nebo ikonického popisu by pro čtenáře bylo obtížné předmět zkonstruovat.



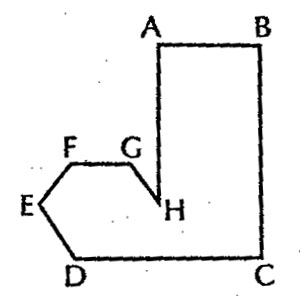
b) Mnohem větší počet studentů si všiml, že předmět obsahuje velkou část obdélníku a velkou část šestiúhelníku, a po tomto zjištění se snažili popsat vztahy mezi těmito dvěma nedokončenými obrazci. z těchto studentů si malá skupina (ale vždy to byl kupodivu alespoň jeden nebo dva studenti ve třídě) všimla, že lze nakreslit úsečku BH a prodloužit ji dál, takže by protínala úsečku DC v bodě I; úsečka HI by potom vytvořila chybějící část šestiúhelníku (Obr.2). Tato imaginární linie by definovala poměr jednotlivých částí obdélníku, ne ovšem jeho skutečné rozměry. Obvykle jsem těmto studentům blahopřál ke schopnosti vytvořit něco, co se podobá mnoha vědeckým hypotézám : "vysvětlit" pozorovatelnou pravidelnost pomocí nějaké imaginární entity.



c) Mnoho zkušených studentů použilo operačního způsobu popisování. Určili si nějaký výsek předmětu (kupodivu dostatečně velký, obvykle to byl úhel) a od něj pokračovali dál, většinou po směru hodinových ručiček, s instrukcemi pro náčrt obrazce.

d) Existují ještě další dvě možnosti popisu, které žádný ze studentů nepoužil. Nikdo například nezačal větou "Předmět je z křídy a tabule". Nikdo také nepoužil metodu autotypu : vytvořit z plochy tabule souřadnicovou síť a zapisovat si "ano", "ne" podle toho, jestli je v daném čtverečku nějaká část obrazce nebo ne. Samozřejmě že pokud by síť byla příliš řídká a předmět malý, spousta informací by nám unikla. (Představte si, že by předmět byl menší než jedna jednotka sítě. Popis by potom obsahoval ne více než čtyři a ne méně než jedno "ano", podle toho, jak by byl předmět v síti umístěn.) Přesto je to způsob, jakým jsou autotypy novinových ilustrací přenášeny elektrickým impulsem nebo jak funguje televize.
Všimněte si, že žádná z těchto metod neposkytuje výklad daného předmětu. Výklad musí vždy vycházet z popisu, a popis musí vždy obsahovat takové charakteristiky, jaké jsme zde uvedli.


6. Divergentní řady nelze předpovědět

Podle klasické představy o vědě lze v podstatě všechno předpovědět a mít pod kontrolou. Pokud to u některých jevů a procesů nejde vzhledem k současnému stavu našich znalostí, za nějaký čas budeme mít něco více vědomostí a hlavně více know-how nám všechny ty 'divoké proměnné' umožní předpovídat a kontrolovat. Tento názor je chybný nejen v podrobnostech, ale z podstaty věci. Můžeme dokonce definovat rozsáhlé třídy jevů, kde je předpověď či kontrola naprosto nemožná ze zcela pochopitelných důvodů. Asi nejznámějším příkladem je rozbití jakéhokoli materiálu, na povrchu homogenního, jako je například sklo. Také Brownův pohyb (viz Glosář) částic v kapalinách a plynech nelze předpovídat.

Když hodím kámen do okna, bude mít prasklina za příslušných podmínek hvězdicovitý tvar. Pokud kámen zasáhne okno tak rychle jako letící střela, pravděpodobně vyrazí ze skla okrouhlou kuželovitou zátku. Jestliže bude kámen moc malý a poletí pomalu, nemusím sklo rozbít vůbec. v tom smyslu je předpověď i kontrola možná. Docela lehce a s jistotou mohu řídit, jakého ze tří výsledků dosáhnu (hvězda, okrouhlý otvor nebo nic), vyhnu-li se mezním oblastem. Avšak v rozsahu podmínek, za kterých rozbiji okno do hvězdicovitého tvaru, je nemožné určit, jaký bude průběh paprsčitých prasklin. Kupodivu, čím bude můj laboratorní postup přesnější, tím nevypočitatelnější bude výsledek. Kdybych použil zcela homogenní sklo, dokonale ho vyleštil a snažil se řídit svůj hod co nejpřesněji, tak aby dopadl na sklo téměř v pravém úhlu, má snaha ještě více znemožní určit výsledek.

Kdybych naopak povrch skla poškrábal nebo použil sklo již prasklé (to bych ovšem podváděl), byl bych schopný do jisté míry předpovědět, jak bude výsledek hodu vypadat. z nějakého důvodu (který mi není znám) půjde prasklina paralelně se škrábnutím asi 1/100 palce do strany, takže škrábnutí bude jen po jedné straně. Dále za ním už nelze směr praskliny předpovědět.

Řetěz se tahem přetrhne v nejslabším místě. To lze předpovědět. Je ovšem těžké určit, který článek řetězu je nejslabší. Obecné můžeme poznat, ale jednotlivé nám uniká. U některých řetězů je předem dáno, za jakého napětí a v kterém místě se přetrhnou. Ale dobrý řetěz je stejnorodý a jakákoliv předpověď je nemožná. Jelikož nevíme, který článek je neslabší, nemůžeme ani vědět, jaké síly je potřeba k jeho přetržení.

Zahříváme-li čistou tekutinu (například čistou destilovanou vodu) v čisté, hladké kádince, kde se na hladině objeví první bublina ? Za jaké teploty ? a v kterém okamžiku ? Tyto otázky nelze zodpovědět, pokud není stěna kádinky mírně poškozená nebo ve vodě není smítko prachu. Není-li žádný takový prvek, který nutně vyvolá změnu, přítomen, nelze předpovědět nic. a protože nevíme, kde dojde ke změně, nemůžeme určit ani, kdy k ní dojde. Tudíž nemůžeme říci, za jaké teploty se voda začne vařit. Pokud je pokus proveden pečlivě - to jest s co nejčistší vodou a co nejhladší kádinkou - dojde k přehřátí. Nakonec se voda začne vařit. Nakonec se vždy objeví nějaký rozdíl, který poslouží jako prvek nutný ke změně stavu. Nakonec si přehřátá kapalina tento rozlišený bod "najde" a bude chvíli bouřlivě vřít, než teplota klesne k bodu varu, odpovídajícímu příslušnému atmosférickému tlaku. Podobné je to i v případě mrznutí kapaliny nebo tvorby krystalů v přesyceném roztoku. Aby proces začal, musí být přítomen prvek, vyvolávající změnu - v případě přesyceného roztoku to může být vskutku mikroskopický krystal.

Na jiném místě knihy se ještě zmíníme o tom, že je veliký rozdíl mezi tvrzeními, které se týkají určitého jednotlivce a tvrzeními o třídě. Věta "Kapalina se vaří" je z jiné úrovně teorie typů než věta "Tato molekula začne první". Tato záležitost je v nejrozmanitějším smyslu významná pro teorii dějin, pro filozofii evoluční teorie a obecně pro pochopení světa, ve kterém žijeme.

Marxistická filozofie, ve své teorii dějin v návaznosti na Tolstého trvá na tom, že velcí mužové, kteří byli jádrem nějakého objevu či hluboké sociální proměny, nejsou vlastně významní pro změny, které vyvolali. Dokazuje například, že v roce 1859 byl celý západní svět zralý (možná přezrálý) k vytvoření a přijetí evoluční teorie, která by odrážela a ospravedlňovala morální základy průmyslové revoluce. v tom smyslu by se dalo říci, že Charles Darwin byl pro vznik evoluční teorie nedůležitý. Kdyby na ni nepřišel on, pak by na něco obdobného přišel někdo jiný v následujících pěti letech. A skutečně, srovnání Darwinovy teorie s teorií Alfreda Russela Wallace se zdá dávat tomuto výroku za pravdu.
Marxisté by tvrdili, pokud tomu dobře rozumím, že existuje nějaký nejslabší článek, že působením příslušných společenských sil a napětí by někdo tu změnu nastartoval a že je úplně jedno, kdo. Ale samozřejmě že to není jedno. Kdyby se místo Darwina prosadil Wallace, měli bychom dnes docela jinou evoluční teorii. Celá kybernetika by se mohla objevit na scéně o nějakých sto let dříve jako výsledek Wallaceova srovnání parního stroje opatřeného regulátorem s procesem přírodního výběru. a nebo by k tomu došlo ve Francii na základě myšlenek Clauda Bernarda, který na konci 19. století objevil to, co bylo později nazváno homeostáze těla. Bernard konstatoval, že tzv. milieu interne - vnitřní prostředí - je vyvážené nebo má samoregulační schopnosti.
       Podle mne je nesmysl tvrdit, že nezáleží na tom, který člověk působí jako prvek, vyvolávající změnu. Právě proto, že na tom záleží, nelze předvídat budoucí vývoj lidstva. Marxistický omyl spočívá v záměně logického typu, ve směšování obecného s jedinečným.


7. Konvergentní řady lze předpovědět

Toto tvrzení je protějškem tvrzení z předchozího oddílu, a jejich vzájemný vztah závisí na protikladu mezi pojmy divergence a konvergence. Tento protiklad je zvláštním, i když zcela zásadním, případem rozdílů mezi jednotlivými stupni Russellovské hierarchie, o které bude řeč ve 4. kapitole. Zatím budiž řečeno jen to, že jednotlivé složky takové hierarchie se mají k sobě navzájem jako člen ke třídě, třída ke třídě tříd, nebo jako pojmenovaná věc ke jménu.

U divergentních řad je důležité, že se vždy jedná o jednotliviny, třeba o jednotlivé molekuly. Místo a čas takových jevů jako je např. prasknutí skla nebo první náznaky varu vody aj. závisí na nějakém okamžitém uspořádání malého počtu jednotlivých molekul. Ani u Brownova pohybu částic nemůže být žádný popis dráhy jednotlivých molekul základem k nějaké další extrapolaci. z toho, co se stane v určitém okamžiku (i kdybychom to mohli vědět), nelze v žádném případě vyvozovat, co se bude dít v okamžiku příštím.

Naopak pohyb planet v sluneční soustavě, průběh chemické reakce v iontovém roztoku solí nebo srážku kulečníkových koulí, do které jsou zapojeny milióny molekul - to vše můžeme předpovědět, protože předmětem našeho zkoumání je v tomto případě chování obrovských shluků nebo celých tříd jednotlivin. Právě tato skutečnost alespoň trochu opravňuje vědu k užívání statistiky, má-li ovšem takový statistik neustále na mysli, že jeho výsledky se týkají výhradně shluků.

Z toho vyplývá, že takzvané zákony pravděpodobnosti se pohybují někde mezi popisem chování jednotlivce a velké skupiny. Jak uvidíme později, tento zvláštní konflikt mezi jednotlivým a hromadným provázel celý vývoj evoluční teorie počínaje Lamarckem. Kdyby byl Lamarck prohlásil, že změny životního prostředí se odrážejí v obecných rysech celých populací, předešel by nejnovější poznatky genetiky, jako jsou např. Waddingtonovy pokusy s genetickou adaptací (viz 6. kapitola). Ale Lamarck a všichni jeho pokračovatelé měli, zdá se, jakýsi vrozený sklon ke směšování logických typů. (Tento problém a z něho vyplývající omyly ortodoxních zastánců evoluční teorie budou podrobněji popsány v 6. kapitole.)

Ať je to tak či onak, u velkých stochastických procesů (viz Glosář) jako je evoluce nebo myšlení, může nové vzejít jen z náhody. a k tomu je zapotřebí určitý proces výběru, aby se dalo nějak vysvětlit, že nová myšlenka je schopna přežít. Něco jako přirozený výběr s celou svou otřepanou tautologií, musí existovat. Aby se nové ujalo, musí být schopno přežít déle než ostatní alternativy. To, co trvá déle ve vlnkách náhody, musí trvat déle než to, co tak dlouho netrvá. To je asi tak v kostce princip teorie přirozeného výběru.

Marxistické pojetí historie - které by, dejme tomu, mohlo tvrdit, že kdyby Darwin nenapsal "Původ druhů", někdo jiný by během pěti dalších let napsal něco podobného - se mylně snaží aplikovat teorii, která nahlíží vývoj společnosti jako konvergentní, na události, týkající se jednotlivých lidských bytostí. Opět další záměna logických typů.


8. "Z ničeho není nic"

Tato citace z "Krále Leara" shrnuje do jediné věty celou řadu středověkých i pozdějších moudrých pouček. Patří k nim :

a) Zákon zachování hmoty a k němu převrácené tvrzení, že žádná nová hmota nemůže vzniknout v laboratoři. b) Zákon zachování energie a k němu převrácené tvrzení, že žádná nová energie nemůže vzniknout v laboratoři. c) Zásada, demonstrovaná Pasteurem, že žádná nová živá hmota nemůže vzniknout v laboratoři. d) Zásada, že žádný nový řád nebo vzor (pattern) nemůže být vytvořen bez informací.

O všech těchto a podobných negativních tvrzeních můžeme říci, že jsou to spíše pravidla očekávání než přírodní zákony. Mají tak blízko k pravdě, že každá výjimka je neobyčejně závažná. Nejzajímavější poznatky se skrývají ve vztazích mezi těmito zásadními negacemi. Dnes už například víme, že mezi zachováním hmoty a zachováním energie existuje spojovací článek, skrze nějž je každá z obou negací sama negována, neboť často dochází k přeměně hmoty v energii a podle všeho i energie v hmotu.

V našem kontextu je ovšem nejdůležitější poslední z řady pouček, totiž zásada, že v oblasti komunikace, organizace, myšlení, učení a evoluce "z ničeho není nic" bez informací. Od zákonů zachování hmoty a energie se liší tím, že neobsahuje žádnou formulaci, která by popírala možnost zničení nebo ztráty informací, vzoru a negativní entropie. Bohužel - ale i naštěstí - vzor (pattern) a informace bývají velice snadno pohlceny náhodou. Zprávy a pokyny důležité pro vytvoření řádu jsou zapsány jen v písku nebo na vodě. Stačí nepatrný pohyb (třeba jen Brownův pohyb částic) a jsou ty tam. Informace se zapomenou nebo znejasní. Klíč se ztratí.

Zprávy přestávají být zprávami, pokud je nikdo není schopen dešifrovat. Bez Rosettské desky bychom se nikdy nedozvěděli, co znamenají egyptské hieroglyfy. Byly by to pro nás jen elegantní ornamenty, nakreslené na papyru nebo vytesané do kamene. Aby měl nějaký pravidelný jev smysl - nebo aby byl dokonce uznán za vzor - musejí se k němu přidružit ještě doplňkové pravidelné jevy, řekněme určité schopnosti, a ty jsou tak pomíjivé jako vzory samy. Jsou také zapsány v písku nebo na vodě. Vývoj schopnosti reagovat na zprávu je druhou stranou procesu evoluce. Je to koevoluce (viz Glosář).

Proti hluboké, leč částečné pravdě, že ve světě informací a uspořádání "z ničeho není nic", mluví však paradoxní skutečnost, že nula, to jest naprostá absence jakéhokoli směrodatného jevu, může být také zprávou. Larva klíštěte vyleze na strom a usadí se na jedné z krajních větví. Když ucítí pot, spadne a zachytí se možná na nějakém savci. Když ale po několik týdnů neucítí žádný pot, spadne také a vyleze si na jiný strom.

Dopis, který jste nenapsali, omluva, kterou jste nevyslovili, jídlo, které jste zapomněli dát kočce - to vše mohou být naprosto dostačující a účinné zprávy, protože nula může mít v určitém kontextu svůj význam; a kontext si vytváří ten, kdo zprávu přijímá. Tato moc vytvářet kontext tkví v dovednosti příjemce; schopnost získat to, co tvoří polovičku jeho koevoluce. Tuto schopnost musí příjemce získat buď poznáním nebo nějakou příznivou mutací, to jest úspěšným útokem na náhodu. Musí být v určitém smyslu připraven učinit náležitý objev v náležitou chvíli.

Takže opak věty, že "z ničeho není nic" bez informace může platit u stochastických procesů. Připravenost může sloužit k výběru určitých složek náhody, které se tak stávají novou informací. Vždy však musí existovat dostatečné množství náhodných jevů, z nichž lze nové informace vytvořit. Na základě této okolnosti se celá oblast uspořádání, evoluce, dospívání a učení dělí do dvou zcela samostatných částí, z nichž jednu tvoří epigeneze nebo embryologie a druhou evoluce a učení. Slovo epigeneze si zvolil C.H. Waddington pro předmět svého zkoumání, jehož původní název zněl embryologie. Nové jméno zdůrazňuje skutečnost, že každé stadium embryologického vývoje je aktem vznikání (řecky genesis), jež musí být vystavěno na (řecky epi) bezprostředně předcházejícím statu quo. Samozřejmě je příznačné, že Waddington pohrdal oficiální, rigorózní informační teorií, neboť podle něj "nové" informace vznikají v každém stadiu epigeneze. a oficiální teorie skutečně existenci nových informací v tomto případě nepřipouštěla.

Epigeneze by se v ideálním případě měla podobat složité tautologii (viz Glosář) : po vyslovení definic a axiomů se už nic nového nepřidává. Pythagorova věta je implicitně přítomna (tj. již zahrnuta) v Eukleidových axiomech, definicích a postulátech. Zapotřebí je pouze vyjádřit ji explicitně a pro lidské bytosti znát pořadí jednotlivých kroků. Tento druh informace je nezbytný až tehdy, je-li Eukleidova tautologie vyjádřena ve slovech či symbolech, seřazených postupně za sebou na papíře nebo v čase. Ale v ideální tautologii neexistuje ani čas, ani explicitnost, ani argumenty. To, co je implicitní, je zkrátka přítomné, přirozeně nikoli v prostoru.

Kromě epigeneze a tautologie, oblastí reprodukce, existuje ještě celý svět tvořivosti, umění, učení a evoluce, kde neustále probíhající procesy změny čerpají z náhody. Podstatou epigeneze je předvídatelné opakování; podstatou učení a evoluce je průzkum (explorace) a proměna. Při předávání kulturních poznatků se lidé vždy snaží reprodukovat, přenést na budoucí generaci schopnosti a hodnoty rodičů; ale tato snaha musí vždy a nutně selhat, neboť předávání kultury probíhá prostřednictvím učení, a ne DNA. Dochází zde k jakémusi míšení obou světů. Při kulturní transmisi je třeba využít fenomén poznávání k reprodukčním účelům, neboť to, co rodiče znají, se museli naučit. Kdyby se nějakým zázrakem stalo, že by děti měli v DNA zakódované schopnosti svých rodičů, byly by to schopnosti jiné a možná nedovolující přežít.

Zajímavé je, že někde mezi oněmi dvěma světy je ještě kulturní fenomén výkladu - to jest zamapování sledu zkoumaných jevů do tautologie. Nakonec budiž řečeno, že svět epigeneze a svět evoluce je určitým způsobem vyjádřen ve dvojím paradigmatu druhého termodynamického zákona. Totiž :

a)

že řád, vzor (pattern) a negativní entropie jsou vždy pohlceny náhodným působením pravděpodobnosti, ale

b)

že pro vytvoření nového řádu působením náhody, je zapořebí velké škály ještě neuskutečněných, alternativních možností (odpovídajících entropii). Evoluce nakonec vede až ke klimaxu - k ekologickému vyčerpání všech možností diferenciace. Učení vede až k přecpání hlavy. Tím, že se přežívající druh vrací zpět k nepoučenému a masově produkovanému vejci, znovu a znovu si vymazává paměť, aby mohl přijímat nové.

9. Číslo není totéž co kvantita

Rozdíl mezi číslem a kvantitou má zásadní význam pro jakékoli teoretizování ve vědě o chování nebo pro nás, chceme-li si představit, co probíhá mezi organismy a uvnitř organismů jako součást procesu jejich myšlení. Čísla jsou výsledkem počítání. Kvantity jsou výsledkem měření. To znamená, že čísla mohou být přesná, protože mezi jednotlivými celými čísly není spojitost. Mezi číslem dvě a tři je skok. U kvantity žádný takový skok není; a protože tam není, nemůže být žádná kvantita naprosto přesná. Můžete mít přesně tři rajčata, ale nikdy ne přesně tři litry vody. Kvantita je vždy jen přibližná.

I když jsme jasně odlišili číslo od kvantity, existuje ještě jeden pojem, který je třeba oddělit od obou. Pro tento pojem myslím neexistuje v moderních jazycích žádný výraz, a tak si jen zapamatujeme, že existuje určitá podskupina vzorů (patterns), jejíž členové se běžně nazývají "čísla". Všechna čísla nejsou totiž výsledkem počítání. Menší a tudíž častěji používaná čísla ve skutečnosti nepočítáme, ale na první pohled je poznáme jako určitý vzor. Karbanící se nezdržují počítáním množství listů v zelené osmě; rozeznají je ihned všechny až do "desítky". Jinými slovy, číslo patří do oblasti vzoru, podoby (gestalt), digitálního počítání; kvantita náleží do světa počítání analogického a pravděpodobnostního.

Někteří ptáci dokáží rozeznat čísla až do sedmi. Nevíme ovšem, zda jde o počítání nebo jen o poznávání určitých vzorů. Rozdíl mezi těmito dvěma způsoby nejdůkladněji prověřil Otto Koehler při pokusech s kavkou obecnou. Naučil ptáka následující cvik : Je dáno určité množství malých hrnků s pokličkou. v hrncích jsou umístěny kousky masa tak, že v některém hrnku je jen jeden kousek, v jiném dva nebo tři a v některém žádný. Odděleně od hrnků je připraven talíř, na kterém je větší počet kousků masa, než je jich celkem ve všech hrncích. Pták se naučí odklopit pokličku u každého hrnku a sníst všechny kousky masa, které v něm jsou. Pak jde k talíři a tam může sníst stejný počet kousků, jaký byl ve všech hrncích dohromady. Když jich sní víc, je potrestán. Tento úkon je pták schopen se naučit.

Otázka tedy zní : Počítá kavka kousky masa nebo používá nějakou jinou metodu, jak rozeznat jejich počet ? Pokus byl nasměrován tak, aby ptáka přinutil počítat. Jeho činnost je přerušována tím, že musí z každého šálku sejmout pokličku a také tím, že počet kousků není ve všech šálcích stejný. Těmito prostředky se Koehler snažil kavce zabránit, aby si vytvořila nějaký vzor nebo rytmus, podle kterého by byla schopná určit počet kousků masa. Byla tedy přinucena je počítat.

Přesto je samozřejmě možné, že si pták vytvoří z odebírání masa v hrncích jakýsi rytmický tanec, který pak opakuje, když si bere maso z talíře. Lze to zajisté zpochybnit; pro mne je však tento výsledek přesvědčivým důkazem pro předpoklad, že pták skutečně kousky masa počítá. Je zajímavé uvažovat o biologickém světě z hlediska následující otázky : Máme různé případy, v nichž je řeč o číslech, považovat za případy číselného počtu nebo pouhé kvantity ? Existuje například dosti zřejmý rozdíl mezi větou "Tato růže má pět korunních plátků, pět kališních lístků a následně i pětičlennou symetrii" a větou "Tato růže má stodvanáct tyčinek, tahle devadesát sedm a tamta jich má jen šedesát čtyři." Proces, který určuje počet tyčinek, se určitě liší od procesu, který upravuje počet plátků či lístků. u plnokvěté růže došlo pravděpodobně k tomu, že se některé tyčinky přeměnily na korunní plátky, takže proces, který určuje, kolik plátků je nutno vytvořit, není normálním procesem vymezení plátků podle pětičetného vzoru, ale spíše procesem, určujícím množství (kvantitu) tyčinek. Můžeme říci, že obyčejná růže má "pět" korunních plátků, ale že má "mnoho" tyčinek, přičemž "mnoho" je kvantita, která se bude u každé růže lišit.

Nyní se můžeme znovu podívat na biologický svět a ptát se, jaké je nejvyšší číslo, s nímž proces růstu pracuje jako s ustáleným vzorem a za nímž už rozeznává jen kvantitu. Pokud vím, u symetrie rostlin a živočichů, zejména u paprskovité symetrie, jsou běžná "čísla" dvě, tři, čtyři a pět. Čtenář teď možná začne se zájmem hledat v přírodě příklady striktně řízených či předem daných čísel. z nějakého důvodu se větší čísla vyskytují jen u lineárních sérií úseků (segmentů) jako je například páteř u savců, břišní články u hmyzu a článkování přední části u žížal. (Přesně je počet článků určen v přední části až po genitální orgány. Čísla se s druhem liší, ale mohou dosáhnout maximálně patnácti. Nad patnáct má ocasní část už jen "mnoho" článků.) k tomu ještě můžeme dodat zajímavou skutečnost, že když si organismus vybere nějaké číslo pro určitou skupinu částí, opakuje toto číslo pak i u částí ostatních. Například lilie má tři kališní lístky a tři korunní plátky, šest tyčinek a trojpouzdrý semeník.

Zdá se, že to, co jsme považovali za nějakou specialitu nebo zvláštnost lidských bytostí - konkrétně to, že my, západní lidé, čísla určujeme počítáním nebo rozeznáváním vzorů a kvantitu určujeme měřením - je všeobecným principem. Viděli jsme, že onen zásadní rozdíl mezi číslem a kvantitou existuje nejen u kavky, ale i třeba u takové růže (u růže v anatomii, u kavky v chování - a samozřejmě v článkování páteře). Co to znamená ? Otázka je to velice stará a objevila se jistě už někde u Pythagora, který se prý s podobnou pravidelností setkal u poměrů mezi alikvotními tóny.

Návod k tomu, jak klást takové otázky, můžeme najít u případu geometrického obrazce z 5. oddílu kapitoly. Tam jsme viděli, že popis se může skládat z nejrůznějších prvků a bylo by naprosto mylné přisuzovat určitému způsobu uspořádání větší hodnotu než jinému. Ale u problému biologických čísel a kvantit jde zřejmě ještě o něco zásadnějšího. Liší se tento případ od případu geometrického obrazce ? a pokud ano, jak ? Soudím, že ani jeden z obou případů není tak jednoduchý, jak se nám zpočátku zdál být problém geometrického obrazce. Vraťme se k věčným pravdám svatého Augustýna. "Slyšte hromová slova světce ze 6. století : 7 a 3 je 10; 7 a 3 bylo vždy 10; 7 a 3 nebylo nikdy nic jiného než 10; 7 a 3 bude vždy 10." Určitě je to tak : tím, že hovořím o rozdílu mezi číslem a kvantitou, blížím se vyjádření nějaké věčné pravdy, a Augustýn by jistě souhlasil.

My ale můžeme světci namítnout : "Jistě, máš pravdu. Ale měl jsi tohle skutečně na mysli ? Je totiž také pravda, že 3 a 7 je 10, a že 2 a 1 a 7 je 10, a že 1 a 1 a 1 a 1 a 1 a 1 a 1 a 1 a 1 a 1 je 10. Ona věčná pravda, kterou jsi se snažil vyjádřit, je ve skutečnosti mnohem obecnější a hlubší než způsob, jakým jsi ji formuloval." Nutno však uznat, že abstraktnější věčnou pravdu by bylo těžké vyjádřit s přesností, jež by nepřipouštěla námitek. Jinými slovy, možná, že všechny způsoby, jak popsat náš geometrický obrazec, jsou jen různými slupkami jediné hlubší a obecnější tautologie (za předpokladu, že eukleidovská geometrie je považována za tautologický systém).

Podle mého je správné tvrdit nejen to, že různé druhy formulování popisu geometrického obrazce se nakonec shodují s tím, co si jejich autoři mysleli, že vidí, ale i to, že existuje shoda v jediné obecnější a hlubší tautologii, na jejímž základě jsou jednotlivé popisy uspořádány. V tom případě je rozdíl mezi číslem a kvantitou netriviální, což dokazuje anatomie růže s jejími "5" korunními plátky a "mnoha" tyčinkami, při čemž já jsem použil při svém popisu růže uvozovky, abych upozornil, že názvy čísel a kvantit jsou jen slupkami formálních idejí, imanentních v rostoucí růži.


10. Kvantita neurčuje vzor

V podstatě není možné vyjádřit vzor pomocí jedné kvantity. Všimněme si však, že již poměr mezi dvěma kvantitami je začátkem vzoru. Jinými slovy, kvantita a vzor náleží k odlišným logickým typům a při jednom stylu uvažování se k sobě příliš nehodí. Problém vývoje vzoru za pomoci kvantity bude jasnější v případě, že vzor je latentně přítomen ještě předtím, než na systém zapůsobila nějaká kvantita. Známý je příklad řetězu, který se působením nějakého napětí roztrhne v nejslabším místě. Díky změně kvantity, tj. napětí, se projeví latentně přítomný rozdíl. Stejné je to i u fotografie - vyvoláním fotografického negativu se projeví latentní rozdíly, které byly do fotografické emulze zaneseny diferenční expozicí diferenční expozicí (tj. vystavení rozdílným osvětlením).

Představte si ostrov a na něm dva kopce. Kvantitativní změna, tj. zvýšení hladiny moře, může z tohoto ostrova udělat dva. Dojde k tomu v místě, kde hladina vody vystoupí nad sedlo mezi kopci. Kvalitativní vzor byl opět latentně přítomen ještě před působením kvantity; ke změně vzoru došlo náhle, jakoby skokem. Populární písemnictví má sklon vysvětlovat vznik vzoru pomocí kvantit jako je napětí, energie a kdoví co ještě. Jsem přesvědčen, že tento přístup je nevhodný nebo dokonce chybný. Z hlediska jakéhokoli činitele, který způsobuje kvantitativní změny, bude každá změna vzoru nepředvídatelná - tedy divergentní.


11. V biologii není monotónních "hodnot"

Monotónní hodnota je taková hodnota, která se buď jen zvyšuje nebo jen snižuje. Její křivka je plynulá, tj. nejsou v ní žádné výkyvy seshora dolů a naopak. Látky, věci, vzory nebo zkušenosti, které jsou pro organismus nějak žádoucí, tj. "dobré" - složení potravy, životní podmínky, teplota, zábava, sex atd. - nemají nikdy takovou povahu, že by více něčeho muselo být nutně lepší než méně. Spíš je pro ně stanoveno množství s optimální hodnotou. Nad tuto hodnotu začíná být látka jedovatá, pod touto hodnotou je jí nedostatek.

Toto pravidlo neplatí pro peníze. Ty jsou vždy ceněny vysoko. Víc peněz je automaticky lepší než míň peněz. Např. 1001 dolarů bude lepší než 1000 dolarů. s biologickými hodnotami je to jinak. Více vápníku nemusí být vždy prospěšnější než méně vápníku. Existuje určité optimální množství, které organismus potřebuje k životu. Je-li vápníku víc, začíná být jedovatý. A stejně je to s kyslíkem, který dýcháme, se složením potravy a snad i se složením vztahů : dostatek je lepší než nadbytek. I takové psychoterapie může být někdy přespříliš. Vztah zcela bez konfliktů je nudný, příliš časté střety působí jako jed. Žádoucí je takový vztah, v němž je určitý optimální podíl konfliktů. Ba dokonce budeme-li uvažovat o penězích ne jako takových, ale z hlediska jejich působení na toho, kdo je vlastní, možná, že zjistíme, že i ty peníze jsou jedovaté, když překročí určitou hodnotu. v každém případě je 'peněžní filosofie', tj. soubor předpokladů, podle nichž je více peněz vždy lepší než méně, naprosto 'antibiologická'. Přesto se zdá, že se jí lze naučit.


12. Malé je mnohdy krásné

Otázku zachování života objasňuje ze všech proměnných snad nejlépe velikost. Slon má problémy s tím, že je moc velký, rejsek zase, že je moc malý. Ale pro každého z nich existuje nějaká optimální velikost. Slonovi by nebylo líp, kdyby byl o hodně menší, a rejskovi by se neulevilo, kdyby vyrostl. Můžeme říci, že u každého se vyvinula jakási 'velikostní' závislost. Existují čistě fyzikální problémy velikosti, které zasahují sluneční soustavu, most nebo náramkové hodinky. Kromě toho jsou tu ale ještě problémy vztahující se výlučně ke shlukům živé hmoty, ať už jde o jednotlivá stvoření nebo celá města.

Podívejme se nejprve do světa fyziky. Problém mechanické nerovnováhy vznikne například, když se přitažlivé síly neřídí stejnými kvantitativními zákonitostmi jako koheze. Větší hrouda hlíny se lépe rozbije o zem než menší. Ledovec neustále roste, přitom zčásti taje a zčásti puká, a proto se začne měnit v laviny, tj. v menší části, které se oddělují od většího celku. A naopak, i malé může být ve fyzikálním světě nestabilní, protože vztah mezi povrchem a váhou není přímo úměrný. Chceme-li nějakou látku rozpustit, nejdřív ji rozbijeme, protože menší kousky mají větší poměr povrchu k objemu, a tudíž do nich rozpouštědlo pronikne lépe. Ty největší kusy se vždy rozpustí jako poslední. A tak dále. Nyní přeneseme tyto myšlenky do složitějšího světa živých bytostí a použijeme k tomu následující historky :

Příběh polyploidního koně

V porotě na udílení Nobelovy ceny prý ještě dnes nastane trapné ticho, když se někdo zmíní o případu polyploidních koní. Nedá se nic dělat, doktor P. U. Posif, velký genetik - utopista, který si trochu pohrál s DNA běžného tažného koně (Equus caballus), toto ocenění za svou práci skutečně získal. Tehdy, koncem 80. let, se říkalo, že velmi přispěl k rozvoji tehdy nové vědy, nazvané 'transportologie'. Ať je to jak chce, dr. Posif dostal cenu za stvoření - jiné slovo se pro tento výtvor aplikované vědy s takřka božskými ambicemi použít nedá - říkám tedy za stvoření koně, přesně dvojnásob většího než je normální hřebec clydesdaleské rasy. Byl dvakrát tak dlouhý, dvakrát tak vysoký a dvakrát tak široký. Byl to polyploid s čtyřnásobným počtem chromozómů.

P.U. Posif nepřestával tvrdit, že byly doby (když byl kůň ještě hříbě), kdy toto báječné stvoření dokázalo stát na všech čtyřech. To musel být úžasný pohled ! Ovšem v době, kdy byl kůň představen veřejnosti a obléhán všemi tehdy existujícími médii, nestál už vůbec. Byl prostě moc těžký. Vážil samozřejmě osmkrát víc než normální tažný kůň.

Dr. Posif trval na tom, aby před veřejností a médii byl kůň bez zvláštních nohavic, které byly nezbytně nutné k udržení jeho normální teploty. To měl potom člověk strach, že se kůň začne uvnitř vařit. To ubohé zvíře mělo kůži a vrstvu podkožního tuku dvakrát tlustší a povrch větší jen čtyřikrát, takže se nestačilo ochlazovat. Každé ráno ho pomocí jakéhosi jeřábu zvedli na všechny čtyři a na lanech ho zavěsili do bedny na kolečkách tak, aby mu na nohou spočívala jen polovina celkové hmotnosti.

Dr. Posif prohlašoval, že zvíře je nadmíru inteligentní. Pravda, mělo osmkrát větší mozek (co se týče váhy) než obyčejný kůň, ale nikdy jsem si nevšiml, že by se zabývalo složitějšími problémy, než jakými se zabývají ostatní koně. Měl celý den co na práci - neustále supěl, jednak proto, aby se ochladil, a jednak, aby zajistil dostatečné množství kyslíku pro své obrovské, osminásobné tělo. Průdušnici měl v průřezu větší jen čtyřikrát. A pak tu bylo jídlo. Musel nějak každý den sníst osmkrát víc potravy a propasovat ji jen čtyřikrát větším jícnem. Cévy měl také relativně úzké, čímž byl ztížen krevní oběh a zvyšoval se tlak na srdce. Chudák kůň.

Tento příběh nám ukazuje, co se nutně stane, když vzájemně reagují dvě nebo více proměnných, jejichž křivky se rozcházejí. Co vzniká interakcí změny a tolerance. Např. neustálý růst počtu obyvatel nebo automobilů nemá zdánlivě žádný vliv na dopravní systém až do chvíle, kdy je najednou práh tolerance překročen a doprava se zablokuje. Změna jedné proměnné odhalí kritickou hodnotu druhé.

Ze všech podobných případů je dnes nejznámější chování štěpné látky v atomové bombě. Uran se běžně vyskytuje v přírodě a neustále se štěpí, ale nikdy nedojde k výbuchu, protože nikdy nevznikne řetězová reakce. Když se rozbije atom uranu, vysílá do prostoru neutrony, které mohou způsobit štěpení, pokud narazí do jiného atomu uranu, ale hodně neutronů se cestou prostě ztratí. Pokud nemá vzorek uranu kritickou velikost, v průměru méně než jeden neutron z každého štěpení narazí do jiného atomu, a řetězec tak postupně zanikne. Je-li vzorek větší, víc neutronů narazí do uranových atomů a způsobí štěpení. Pochod dosáhne exponenciálního růstu a dojde k výbuchu.

V případě našeho koně došlo k nesouladu (diskrepanci) mezi délkou, povrchem a objemem (a tedy i hmotností), byly vzájemně v rozporu, neboť jejich hodnoty rostly se vzájemně nelineární úměrností : povrch se mění se čtvercem délky, objem s třetí mocninou délky a povrch s 2/3 mocninou objemu. Kůň, (a vůbec žádná živá bytost), to nemá lehké, protože musí udržovat v chodu bezpočet vnitřních funkcí, aby se udržel naživu. Existuje vnitřní logistika sítě vzájemností mezi krví, potravou, kyslíkem a výměšky, a podobně mezi informacemi, přenášenými neurony nebo hormony.

Sviňucha obecná, asi metr dlouhá, s vrstvou podkožního tuku širokou asi 2,5 cm a povrchem asi 1,8 m², hospodaří s teplem způsobem, který je výhodný pro pohyb v Arktických mořích. Tepelný systém velryby, která je asi desetkrát delší než sviňucha (tj. má tisíckrát větší objem a stokrát větší povrch), s vrstvou tuku asi 30 cm, je naprostou záhadou. u kytovců pravděpodobně existuje nějaká vyšší logistika oběhu krve skrz hřbetní a ocasní ploutve, pomocí níž se zbavují přebytečného tepla. Růst je dalším faktorem, který komplikuje již tak složitou otázku velikosti u živých bytostí. Mění se během růstu poměr mezi jednotlivými částmi organismu ? Problém omezení růstu řeší různé druhy rostlin a živočichů různě.

Nejjednodušší je asi případ palem, které nepřizpůsobují šířku kmene své výšce. Takový dub, s růstovou tkání (kambiem) ve dřevě i v kůře, roste celý život do výšky i do šířky. Ale kokosová palma má růstovou tkáň jen na vrcholku kmene (je to tzv. salát milionářů, protože když se odkrojí, rostlina zahyne), a tak je prostě stále vyšší a vyšší, a kmen se nepatrně rozšiřuje jen u kořene. Pro tento organismus je výškové omezení normální součástí adaptace. Rostlina obvykle hyne v důsledku prosté mechanické nestability způsobené nadměrnou výškou, která není vyvážena tloušťkou kmene.

Mnohé rostliny obcházejí problémy spojené s omezením růstu tím, že délku života spojí s kalendářem nebo s vlastním reprodukčním cyklem. Jednoleté rostliny plodí nové generace každý rok, a naopak takové rostliny jako je juka, mohou žít mnoho let, ale stejně jako losos umírají při rozmnožování. Kromě kvetoucího vrcholku, který je bohatě rozvětvený, juka žádné větve nevytváří. Rozvětvené květenství je poslední částí kmene, a když splní svou funkci, rostlina umírá. Její smrt odpovídá způsobu jejího života. U některých vyšších živočichů je růst přísně regulován. V určité velikosti, věku nebo stadiu vývoje živočich prostě přestane růst (tj. jeho růst je zastaven na základě chemických nebo jiných informací, vycházejících z vnitřního uspořádání organismu). Regulované buňky přestanou růst a dělit se.

Přestane-li regulace fungovat (na základě selhání schopnosti vysílat nebo přijímat informace), výsledkem je rakovina. Kde takové zprávy vznikají ? Co je pohání a v jakém chemickém kódu jsou uloženy ? Čím je řízena téměř dokonalá vnější bilaterální symetrie u savců ? Víme toho až podivuhodně málo o systému zpráv, který řídí růst. Musí to být systém dost složitě propojený, o kterém nemáme zatím téměř tušení.


13. Logika nevyjadřuje přesně vztah příčiny a následku

Jsme zvyklí užívat stejné výrazy pro sled logických tvrzení, jako pro sled příčin a následků. Říkáme : "Jestliže platí Eukleidovy definice a postuláty, pak dva trojúhelníky, kde součet tří stran jednoho trojúhelníku se rovná součtu tří stran druhého trojúhelníku, jsou si rovny." Anebo : "Jestliže teplota klesne pod 0°C, pak se voda začne měnit v led." Ale logické jestliže...pak v sylogismu se velice liší od jestliže...pak u příčiny a následku.

V počítači, který pracuje na základě příčiny a následku tak, že jeden tranzistor spouští druhý, se příčinného řetězce používá k simulování logiky. Před třiceti lety jsme se ptávali : Může počítač napodobit všechny logické postupy ? Odpověď zněla ano, ale otázka byla špatně položena. Měli jsme se spíše ptát : Může logika napodobit všechny vztahy příčiny a následku ? a odpověď by zněla ne.

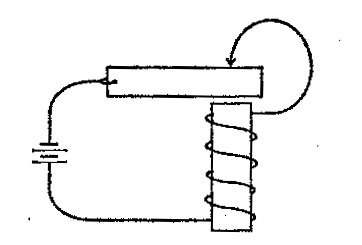
Pokud řetězce příčiny a následku začnou probíhat v kruhu (nebo ještě složitěji), při popisu nebo zaznamenání řetězce do bezčasé logiky vzniknou protimluvy; paradoxy, které čistá logika nemůže připustit. Za příklad těchto zřejmých paradoxů nám poslouží obyčejný elektrický obvod u zvonku, za příklad jediný, zatímco u biologické homeostáze jsou jich milióny. Obvod (viz obr. 3) je sestrojen tak, že v okamžiku, kdy se kotva spojí s elektrodou v bodě A, začne obvodem procházet elektrický proud. Proud však aktivuje elektromagnet, který kotvu oddálí a přeruší tím kontakt v bodě A. Proud je přerušen, elektromagnet přestane být aktivován, kotva se vrátí, obnoví kontakt v bodě a a cyklus se opakuje.



Vyjádříme-li jej v řetězci příčin a následků, dostaneme :

Jestliže se vytvoří kontakt v bodě A, pak je magnet aktivován.

Jestliže je magnet aktivován, pak je kontakt v bodě A přerušen.

Jestliže je kontakt v bodě a přerušen, pak magnet není aktivován.

Jestliže magnet není aktivován, vytvoří se kontakt.

Taková posloupnost naprosto vyhovuje, pokud jsme si jasně vědomi, že vztah jestliže...pak je příčinný. Kdyby ale někdo z žertu přenesl všechna ta jestliže a pak do říše logiky, způsobil by tam pořádný zmatek :

Jestliže se vytvoří kontakt, pak je kontakt přerušen.

Jestliže P, pak non P.

V příčinném spojení jestliže...pak je přítomen čas, ale stejné spojení v logice je bezčasé. z toho vyplývá, že logika není přesným vyjádřením příčiny a následku.


14. Příčinnost nefunguje zpětně

Logické věty lze často převrátit, ale následek nikdy nepředchází příčinu. v tom je kámen úrazu pro psychologické i biologické vědy již od dob Platóna a Aristotela. Staří Řekové rádi věřili tomu, co bylo později pojmenováno jako konečné příčiny. Věřili, že vzor (pattern), vytvořený na konci nějakého sledu událostí, lze v jistém smyslu považovat za příčinu dění, které následuje. z toho pak vzniklo celé učení, zvané teleologie (telos = cíl nebo účel).

Problém, s nímž se potýkali biologové, se týkal adaptace. Zjistilo se např., že krab má klepeta, aby do nich mohl uchopovat předměty. Potíže nastaly, když se začalo argumentovat zpětně od účelu klepet k příčině jejich vzniku. Dlouhou dobu se v biologii považovalo za kacířské věřit, že klepeta vznikají, protože jsou užitečná. Tato myšlenka byla teleologickým omylem, neboť převracela časovou posloupnost příčiny a následku. Lineální myšlení vždy povede bu¦ k teleologickému omylu (že proces je určen cílem) nebo k mýtu o nějakém nadpřirozeném, vše řídícím činiteli.

Ve skutečnosti jestliže se soustava příčin a následků octne v kruhu (viz dále ve 4. kapitole), může být jakákoli změna v jedné části cyklu považována za příčinu změny jakékoli proměnné v následujícím čase kdekoli uvnitř cyklu. Takže zvýšení teploty v místnosti lze považovat za příčinu změny v termostatu, a naopak, činnost termostatu v jistém smyslu reguluje teplotu v místnosti.


15. Jazyk obvykle zdůrazňuje jen jednu část každé interakce

Obyčejně mluvíme tak, jako by nějaká "věc" "měla" určité vlastnosti. Říkáme, že kámen je "tvrdý", "malý", "těžký", "žlutý", "hustý", "křehký", "horký", "pohyblivý", "nehybný", "viditelný", "jedlý", "nejedlý", atd. Tak je náš jazyk utvářen. "Kámen je tvrdý." Takový způsob řeči se hodí na tržiště : "To je nová značka." "Brambory jsou shnilé." "Vejce jsou čerstvá." "Popelnice je rozbitá." "Diamant je porušený." a tak dále.

Nehodí se ale dost dobře pro vědu či epistemologii. Abychom správně mysleli, je dobré předpokládat, že všechny vlastnosti, znaky, přívlastky atd. se vztahují nejméně ke dvěma řadám interakcí v čase. "Kámen je tvrdý" znamená, a) že je těžké ho nějakým způsobem prorazit nebo provrtat, b) že následkem určitých nepřetržitých interakcí mezi molekulárními částicemi drží tyto částice pevně pohromadě. "Kámen je nehybný" popisuje pozici kamene vzhledem k postavení mluvčího nebo dalších pohybujících se předmětů. Vyjadřuje také určité stavy nebo vlastnosti kamene : jeho inercii, nepřítomnost vnitřního porušení, povrchového tření apod.

Jazyk pomocí svého subjekt-predikátového systému neustále opakuje, že "věci" "mají" vlastnosti a znaky. Přesnější by bylo zdůrazňovat, že "věci" vznikají a jsou nahlíženy odděleně od jiných "věcí", a že se stávají "skutečnými" na základě vnitřních vztahů a svého chování ve vztahu k jiným věcem a k mluvčímu. Je třeba, abychom si pevně vštípili obecný princip, že čímkoli jsou "věci" ve svém pleromatickém světě, do světa dorozumívání a významu mohou vstoupit svými jmény, vlastnostmi a přívlastky (tj. skrze informace o svých vnitřních i vnějších vztazích a vzájemném působení).


16. "Stabilita" a "změna" popisují části našeho popisu

V dalších částech knihy bude slovo stabilní, a tím i slovo změna, hrát velmi důležitou úlohu. Bylo by proto rozumné prozkoumat podrobně oba výrazy již v této, úvodní části a zjistit, jaké záludnosti v sobě skrývají. Adjektivum stabilní se většinou používá při popisu věcí. Stabilní může být chemická sloučenina, dům, ekosystém nebo vláda. Půjdeme-li ještě dál, narazíme na definici, že stabilní předmět je takový předmět, který se nemění působením či tlakem nějaké zvláštní vnější nebo vnitřní okolnosti, případně že odolává náporům času.

Začneme-li pátrat, co se skrývá za tímto významem slova, nalezneme celou řadu mechanismů. Nejjednodušším z nich jsou fyzikální tvrdost a viskozita, vlastnosti, které popisují působení mezi stabilním předmětem a nějakým jiným předmětem. Na vyšších, složitějších úrovních je to pak obrovské množství vzájemně propojených procesů, kterým se říká život, a ty udržují náš předmět v proměnlivém stavu, v němž ale přece jen existují nějaké nezbytné konstanty, jako je tělesná teplota, krevní oběh, hladina cukru v krvi nebo dokonce život sám. Akrobat na vysokém laně si udržuje stabilitu neustálou korekcí své nerovnováhy.

Tyto složitější případy naznačují, že když mluvíme o stabilitě v souvislosti s živými bytostmi nebo samoopravnými cykly, měli bychom se řídit příkladem těch jsoucen, o nichž hovoříme. Pro akrobata na laně je důležitá jeho tzv. "rovnováha"; pro savce bude stejně důležitá "teplota". Změny těchto proměnných jsou v každém okamžiku přenášeny do komunikačního systému v těle. Abychom se tedy řídili příkladem dané entity, měli bychom vždy definovat stabilitu pomocí nějakého stále platného popisného tvrzení. Věta "Akrobat je na vysokém laně" nepřestává být pravdivá ani při působení slabých závanů větru nebo vibrací provazu. Tato "stabilita" je výsledkem neustálých změn v popisu akrobatovy pozice a pozice jeho tyče.

Z toho vyplývá, že kdykoli hovoříme o živých entitách, výpovědi týkající se "stability" by měly vždy odkazovat k nějakému popisnému tvrzení, aby logický typ slova "stabilní" byl zřejmý. Později, zejména ve 4. kapitole, uvidíme, že každé popisné tvrzení má být charakterizováno podle logického typu podmětu, přísudku a kontextu. Také všechny výpovědi o změně vyžadují podobné upřesnění. Takové hlubokomyslné pravdy jako je francouzské "Plus a change, plus c'est la m#me chose" (Čím víc se to mění, tím je to stejnější) vděčí za svou mudrlantskou všeplatnost jen a jen smíchání logických typů. Co "se mění" a co "je stejné", to jsou popisná tvrzení, ale každé jiného řádu.

Nyní je potřeba říci ještě něco k seznamu předpokladů, probraných v této kapitole. Za prvé, tento seznam není v žádném smyslu úplný a autor knihy nepředpokládá, že by něco takového jako úplný seznam všech pravd či obecných tvrzení mohlo být vůbec sestaveno. Vyplývá snad z charakteru světa, v němž žijeme, že by takový seznam měl být konečný ? Při přípravě této kapitoly jsem asi 12 dalších předpokladů vyřadil a množství jiných jsem přesunul do kapitoly 3., 4. a 5. I přes tuto neúplnost si však čtenář může se seznamem vyzkoušet několik cvičení.

První věcí, kterou udělá vědec s takovým seznamem, je, že začne třídit a řadit za sebe jednotlivé části. To jsem částečně udělal sám a rozdělil jsem seznam do čtyř částí, jejichž podskupiny se k sobě pojí různým způsobem. Bylo by nesnadné vypočítat všechny způsoby, jakými mohou být tyto pravdy či předpoklady spolu spojeny. Já jsem zvolil následující seskupení : V první skupině jsou oddíly 1 až 5, neboť popisují různé aspekty nutně přítomného fenoménu kódování. Zde například lze dosti lehce rozpoznat, že věta "věda nikdy nic nedokazuje" je synonymem k rozdílu mezi mapou a mapovaným územím; obě vyplývají z Amesových pokusů a z obecného tvrzení přírodovědy, že "neexistuje žádná objektivní zkušenost".

Je zajímavé, že z abstraktního a filosofického hlediska se tato skupina obecných tvrzení musí velice úzce pojit s něčím jako je Occamova břitva nebo zákon o "ekonomii myšlení" ('zákon úspornosti'). Bez tak rozhodujícího kritéria by neexistoval žádný rozhodující způsob, jak si vybrat mezi jednotlivými hypotézami. Jakožto nezbytné bylo stanoveno kritérium jednoduchosti proti složitosti. Ovšem vedle těchto obecných tvrzení je tu ještě jejich spojitost s neurofyziologií, Amesovými pokusy a podobně. Člověka hned napadne, zda látka, týkající se vnímání, nesouvisí s nějakou filosofičtější látkou, protože v procesu vnímání je přítomno něco jako Occamova břitva či kritérium úspornosti myšlení. Debata o částech a celcích v 5. oddíle je vyjádřením běžné formy transformace, ke které dochází při procesech, nazvaných popis.

Druhou skupinu tvoří oddíly 6, 7 a 8, které se zabývají otázkami náhody a řádu. Čtenář si může všimnout, že tvrzení, že nové může vzejít jen z náhody, je skoro úplně v protikladu k nevyhnutelnosti entropie. Celý problém entropie, negentropie (viz Glosář) a rozporů mezi řadou obecných tvrzení, spojených s těmito slovy a tvrzení týkajících se energie, bude předmětem diskuse v 6. kapitole, kde se hovoří o ekonomické stránce přizpůsobivosti. Zde si jen povšimněme zajímavé formální analogie mezi zřejmým rozporem v této skupině a rozlišením, které v 9. oddíle, tj. ve třetí skupině, jasně odděluje číslo od kvantity. Způsob myšlení, který se zabývá kvantitou, se v mnoha ohledech podobá myšlení, točícímu se kolem pojmu energie; kdežto pojem čísla má mnohem blíže k pojmům vzoru (pattern) a negentropie. Základní tajemství evoluce spočívá samozřejmě v rozporu mezi tezemi druhého termodynamického zákona a zjištěním, že nové může vzejít jen z náhody. Právě tento rozpor vyřešil zčásti Darwin svou teorií přirozeného výběru.

Další dvě skupiny představují oddíly 9-12 a 13-16. Nechám na čtenáři, aby si sám formuloval, jak jsou tyto skupiny vnitřně propojeny, a aby si případně sestavil jiné skupiny podle svého vlastního způsobu myšlení. Ve 3. kapitole budu pokračovat v náčrtu pozadí své teze pomocí řady dalších obecných tvrzení či předpokladů. Tentokrát se však již přiblížím k ústředním problémům myšlení a evoluce, neboť se pokusím odpovědět na otázku : Jakými způsoby mohou dvě nebo více informací či příkazů působit společně nebo proti sobě ? Tato otázka a její nesčetná řešení jsou podle mého zásadním bodem každé teorie myšlení či evoluce.