 O nás
Obsah
Archiv
Partneři
Zajímavé weby
Kontakty
O nás
Obsah
Archiv
Partneři
Zajímavé weby
Kontakty

Světoznámý český matematik emeritní profesor University Karlovy Petr Vopěnka je širší veřejnosti znám jako autor skutečně monumentálního díla o dějinách matematiky, nazvaného „Úhelný kámen evropské vzdělanosti a moci“, které vznikalo v období let 1981 až1996 a které je podloženo hlubokým studiem matematiky, historie, filosofie a veškerého vědění a umění té které doby.
Dějinám matematického myšlení se věnuje již velmi dlouhou dobu a pod jeho vedením byla již přeložena řada klasických matematických děl do češtiny. Profesor Petr Vopěnka pochází z pedagogické rodiny a na začátku devadesátých let působil krátkou dobu jako ministr školství mládeže a tělovýchovy a úroveň české vzdělanosti mu stále nedává spát. V prvním čísle časopisu Vhled z roku 2014 jsme zveřejnili přednášku „Matematika a vzdělávání“, kterou profesor Petr Vopěnka přednesl na Konferenci Jednoty českých matematiků v roce 2007. Jak vidíme je stále aktuální.
V druhém čísle obnoveného časopisu Vhled jsme přinesli ukázku z jeho stěžejního díla „Úhelný kámen evropské vzdělanosti a moci“. Ve třetím čísle obnoveného časopisu Vhled jsme zveřejnili ukázku z knihy nazvané „Příležitostné rozpravy s matematikou“, kterou vydalo podnětné nakladatelství OPS (www.o-p-s.cz). Za mimořádnou ochotu v tomto směru děkujeme panu Michalu V. Hanzelínovi, který stojí v jeho čele.
V minulém roce nás profesor Petr Vopěnka navždy opustil a zatím tedy nabízíme jeho věrným čtenářům alespoň fragment z jednoho díla, kterým se v poslední době zabýval. Za zprostředkování děkujeme panu Michalu V. Hanzelínovi a za souhlas ke zveřejnění dědici autorských práv profesora Petra Vopěnky, jeho synovi, nakladateli a spisovateli Martinu Vopěnkovi.

| Fragment úvodu profesora Petra Vopěnky k 13. Eukleidově knize |
Petr Vopěnka |
| Timaiova osnova reálného světa |
|
| Scholion |
| Čísla, rozumí se stále jen malá nebo alespoň nevelká, mají na hloubavé lidi zvláštní (magický) vliv. Setkáváme se s nimi téměř na každém kroku, a to v nejrůznějších souvislostech, kdy nás vyzývají, abychom s nimi konfrontovali a seřídili naše myšlení a konání. … S některými výskyty čísel jsme se již setkali, některé další ještě uvedeme. Samozřejmě ne všechny, neboť jich je nepřeberné množství. Rozhodně by ale stálo za to sestavit jakýsi atlas pokud možno co největšího množství výskytů čísel jak v reálném světě, tak i v lidském myšlení. Ne všechny výskyty téhož čísla jsou rovnocenné. | |
| Petr Vopěnka |
Téměř hned na popisu pravidelných mnohostěnů a zjemněné struktury jejich stěn (viz konec pátého oddílu) pokračuje Timaiův výklad takto:
Rozdělme tvary, které v našem výkladu vznikly, mezi oheň a zemi a vodu a vzduch. Zemi pak dejme tvar krychle; neboť země je ze všech čtyř živlů nejméně pohyblivá a z hmot nejtvárnější: takové pak musí býti to, co má nejstálejší plochy. Přirozeně pak jest plocha trojúhelníků na počátku předpokládaných, rovnoramenných, pevnější ne trojúhelníků nerovnoramenných a z plošných obrazců složených z těch obojích trojúhelníků rovnostranný čtyřúhelník rovinný nutně stojí – jak do částí, tak i v celku – stáleji než rovnostranný trojúhelník.
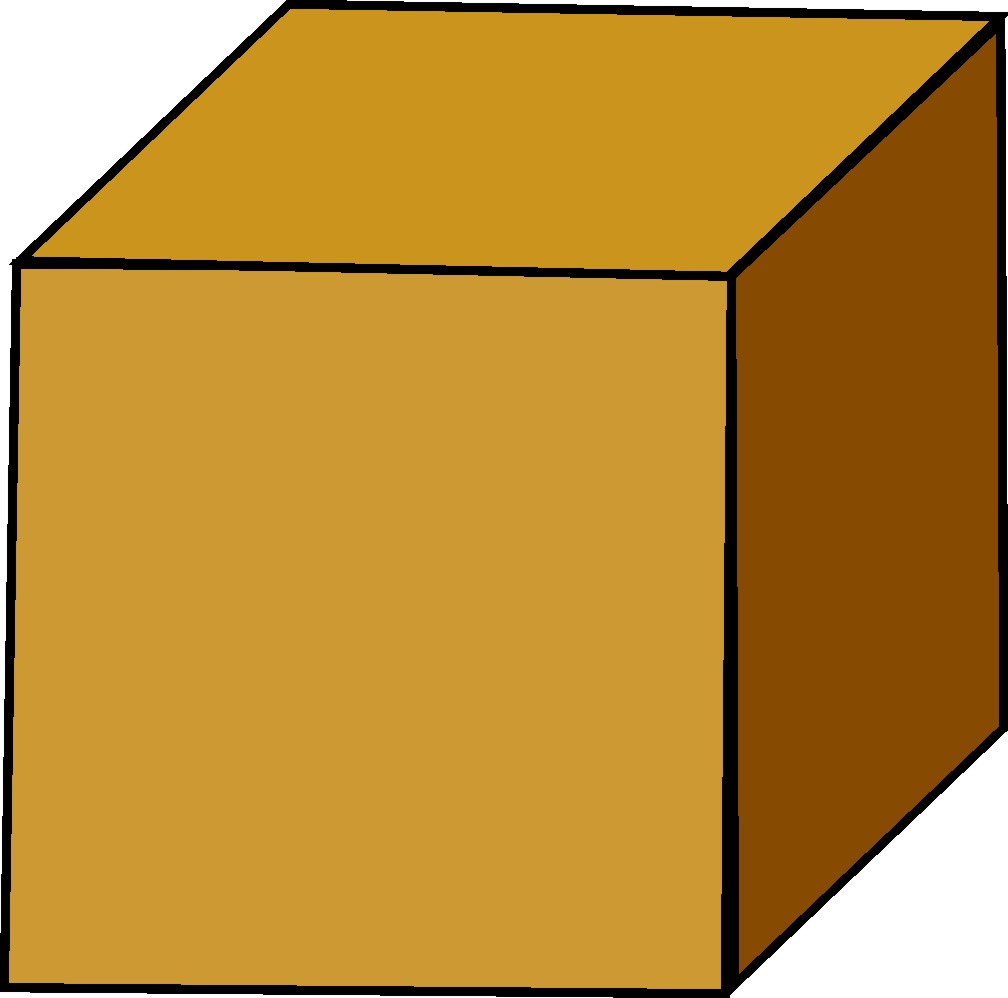 |
| Krychle |
Proto přidělujíce tento tvar Zemi, zachováváme pravděpodobnost; naopak zase vodě dejme nejméně pohyblivý z ostatních tvarů, nejpohyblivější pak ohni a střední vzduchu; a nejmenší tělo ohni, největší zase vodě a střední vzduchu; a zase nejostřejší ohni, druhé pak vzduchu, třetí vodě. Ze všech těchto živlů ten, který má nejméně ploch, jest jistě nejpohyblivější, ze všech nejbřitčí a vůbec nejostřejší, dále pak nejlehčí, poněvadž je složen z nejmenšího počtu týchž částí; druhý živel co do týchž vlastností jest na druhém místě, třetí pak na třetím.
Bylo by tedy podle správného soudu i podle pravděpodobnosti těleso tvaru jehlance prvek a zárodek ohně; tvar co do vzniku po tomto druhý řekněme, že náleží vzduchu, třetí pak vodě. Všechna tato tělíska jest si mysliti malá, že jednotlivé částečky každého živlu pro jejich nepatrnost nevidíme, ale když se jich skupí mnoho, vidíme jejich shluky; a co se týče jejich poměrů a množství i pohybů a ostatních vlastností, jest souditi, že demiurg, pokud jen přirozená podstata nutnosti dobrovolně a přemluvena to dovolovala, potud je přesně vytvořil, a tím uvedl tyto živly v promyšlený soulad. Poněvadž byl ještě jed, pátý, pravidelný mnohostěn, pravidelný dvanáctistěn, užil ho demiurg propracovávaje nákres všehomíra.
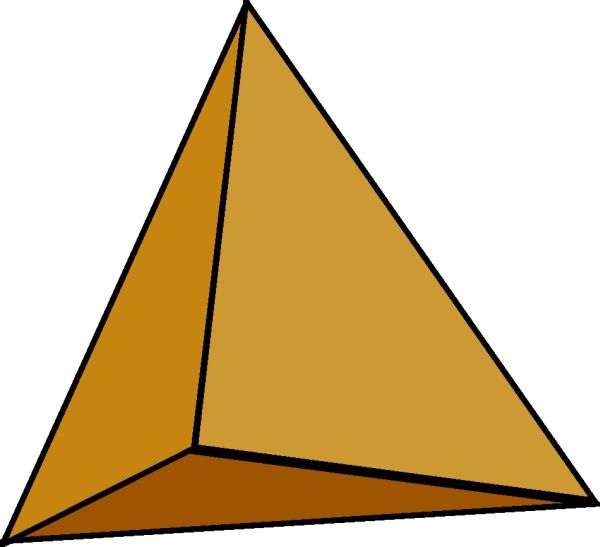 |
| Jehlan |
Právě oboustranné poukazy mezi jednotlivými abstrahovanými živly a timaiovskými mnohostěny (země – krychle, voda – dvacetistěn, vzduch – osmistěn, oheň – čtyřstěn) jsou tedy základem Timaiovy osnovy, podle níž demiurg budoval reálný svět.
Jak je patrno, uvedené poukazy a následná i z nich vytvářená osnova reálného světa, se nacházejí v onom prostředním světě ležícím mezi světem reálným a světem idejí. S touto osnovou můžeme tedy zacházet stejně jako zachází s antickým geometrickým světem; rozvíjet ji, zkoumat ji, a podobně.
Toho využil Timaios, když předvedl, že nejde jen o nějaké náhodné poukazy, ale o hlubší analogii, takže osnova, kterou vytvořil, umožňuje dokonce (tak jako antický geometrický svět) získávat poznatky o reálném světě. K tomu účelu využil prve uvedené rozklady rovnostranného trojúhelníka na šest (tedy nikoli jen na dva) timaiovské trojúhelníky a čtverce na čtyři (tedy nikoli jen na dva) pravoúhlé rovnostranné trojúhelníky. To mu pak umožnilo volněji zacházet s oběma dokonalými pravoúhlými trojúhelníky: skládat z nich různé další útvary a hledat jejich analogie v reálném světě (viz následující dva odstavce opsané ze zkoumaného Platonova dialogu).Toho využil Timaios, když předvedl, že nejde jen o nějaké náhodné poukazy, ale o hlubší analogii, takže osnova, kterou vytvořil, umožňuje dokonce (tak jako antický geometrický svět) získávat poznatky o reálném světě. K tomu účelu využil prve uvedené rozklady rovnostranného trojúhelníka na šest (tedy nikoli jen na dva) timaiovské trojúhelníky a čtverce na čtyři (tedy nikoli jen na dva) pravoúhlé rovnostranné trojúhelníky. To mu pak umožnilo volněji zacházet s oběma dokonalými pravoúhlými trojúhelníky: skládat z nich různé další útvary a hledat jejich analogie v reálném světě (viz následující dva odstavce opsané ze zkoumaného Platonova dialogu).
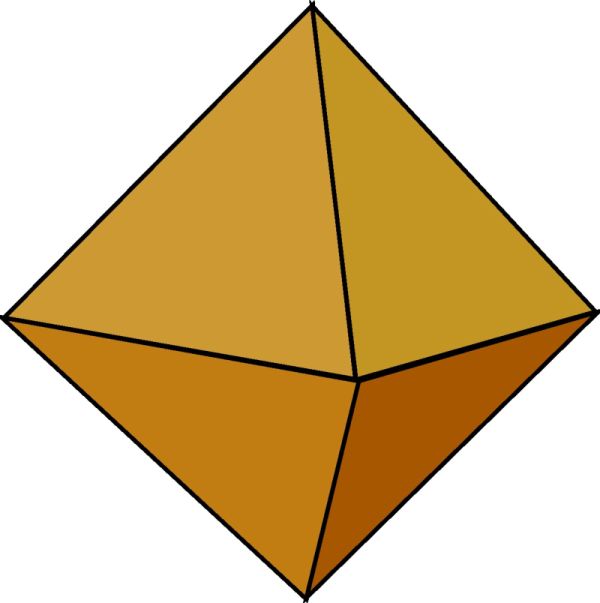 |
| Osmistěn |
Podle všeho, co jsme řekli, mělo by se to s živly pravděpodobně nejspíše takto: Země, setká-li se s ohněm, bývá rozloučena jeho ostrostí a jest unášena – ať by už byla rozpuštěna v samém ohni nebo ve hmotě vzduchu nebo vody, až by její částice někde se setkajíce opět se vespolek spojily a staly se zemí; neboť do jiného tvaru by nikdy nemohly přejíti. Voda však, rozdělena ohněm nebo i vzduchem, může složením dáti vznik jednomu tělísku ohně a dvěma vzduchu; co se pak týče rozkladu vzduchu, z jedné rozloučené částice vznikla by dvě tělíska ohně. A naopak, kdykoli oheň, obsažený ve vzduchu, ve vodě nebo někde v zemi, a to malým množstvím v jejich velkém množství, unášen jsa jejich pohybem, bojuje a jsa přemožen se rozkládá, dvě těla ohně seskupují se v jeden tvar vzduchu; a když jest přemožen vzduch a rozkouskován, z dvou celých dílů a polovice bude jeden celistvý tvar vody. Uvažme totiž o tom zase ještě takto: kdykoli oheň zachvátí některý z ostatních živlů a rozřízne jej ostrostí svých rohů a hran, onen živel přestává býti řezán, jakmile se složí v přirozenou podstatu ohně – neboť každý jednotlivý druh jsoucna sobě podobný a se sebou totožný nemůže v totožném a podobném způsobiti nějaké změny, ani se s ním nemůže nic státi působením něčeho takového, pokud však naráží na něco jiného a sám jsa slabší bojuje s ním silnějším, nepřestává býti rozlučován. Na druhé straně zase kdykoli malé množství meších tělísek, objímáno četnými většími, jest tříštěno a hasne, přestává hasnouti, chce-li složiti v podobu prvku vítězného, a stává se z ohně vzduchem, ze vzduchu vodou; pakli však vchází v zápas s rovnými silami a některý z ostatních prvků se s ním v boji sráží, rozlučování neustává, dříve, než buď jedno nebo druhé úplně jsouc zatlačeno a rozloučeno unikne k prvku příbuznému, anebo jsouc přemoženo, spojí se jsoucno podobné vítězi a zůstane trvale s ním. Podle těchto stavů mění všechno také svá místa; neboť hromady každého jednotlivého druhu jsou působením pohybu přijímatelčina rozloženy po různu na vlastním místě, a tu ony živly, které kdy ztrácejí podobnost se sebou samými a připodobňují se jiným, jsou jejím otřásání zanášeny na místo oněch, ke kterým se připodobní.
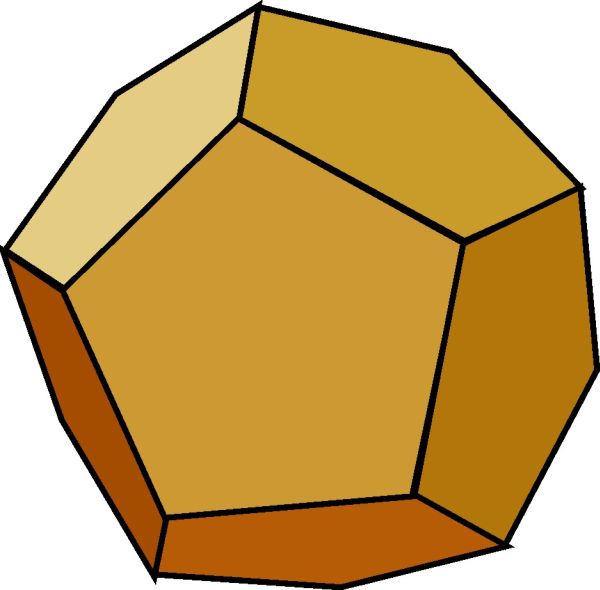 |
| Dvanáctistěn |
Všechny nesmíšené a prvotní látky vznikly tedy z takovýchto příčin; že však v jejich rodech se utvořily zvláštní druhy, toho příčinu jest viděti ve složení jednoho i druhého prvku; neboť nevytvořil se na počátku jen jeden trojúhelník o jedné velikosti, nýbrž menší a větší, počtem tolikeré, kolik jest druhů v oněch živlech. Proto tedy v jejich míšení, jednak samých mezi sebou, jednak vespolek s jinými, jest nekonečná rozmanitost; tuto třeba pozorovati, chceme-li pravděpodobně vykládati o přírodě.
Hlavním předmětem zájmu platónských myslitelů je svět idejí. Nejschůdnější cesta k idejím tvaru a velikosti vede skrze (antický) geometrický svět neboli na objektech tohoto světa se ideje ukazují v průzračné čistotě. Tyto ideje jsou ovšem přítomny i ve světě reálném, tam však jsou zatemněné i jsou tam znečištěné látkou, která na těchto objektech lpí. Platónský myslitel tedy z geometrického světa čerpá poznatky o idejích, ze světa reálného pak nanejvýše podněty.
Timaios veden záměrem, který si předsevzal, vymezil v geometrickém světě oblast složenou z timaiovských mnohostěnů, čtverců, trojúhelníků rovnostranných, pravoúhlých rovnoramenných a timaiovských. Rozkládání a skládání těchto objektů je tedy stále ještě pěstování čisté geometrie v geometrickém světě.
 |
| Dvacetistěn |
Rozšířením geometrického světa o ideální abstrahované živly a o poukazy mezi nimi a timaiovskými mnohostěny, nalezl Timaios prostřední svět, který je obsáhlejší než svět geometrický. Podnět k nalezení tohoto světa, stejně jako směr jeho zkoumání, vyšly pochopitelně ze světa reálného.
Timaiovým záměrem však nebylo nalezení takového ideálního prostředního světa, který by byl vhodným východiskem ke studiu světa idejí, ale naopak takového, který by byl vhodným nástrojem ke studiu světa reálného, které pak začal provádět podle prve uvedené osnovy. Posuzováno pouze z tohoto úzkého hlediska, šlo vlastně o vulgarizaci záměrů Pythagorových, a zvláště pak Platonových.
Na druhé straně právě takovéto vulgarizace byly nesmírně podnětné pro rozvoj vědy o reálném světě, a to během celého jejího vývoje. Díky nim pronikaly Platonovy ideje do reálného světa, takže se mnohé z nich usadily jako jeho součásti, podobně jako se později například geometrický prostor stal prostorem reálným. Dokonce lze tvrdit, že celá novověká evropská věda je na těchto vulgarizacích založena. Ukáže-li se, že některá taková vulgarizace je nevhodná, okamžitě ji vědci nahradí jinou, vhodnější.